SuperSmoother

The supersmoother is a non-parametric adaptive smoother which has been used within the astronomical literature as an estimator of periodic content. For each candidate frequency, the supersmoother algorithm is applied to the phased data and the model scatter is computed. The period for which the model error is minimized is reported as the best period.

Single-band Supersmoother

The standard, single-band supersmoother is implemented in the SuperSmoother algorithm. The main parts of the API discussion from Lomb-Scargle Periodogram apply here as well. Here is an example of using the supersmoother to find the best period of an RR Lyrae star. Note that the supersmoother algorithm is much slower than even the slow version of Lomb Scargle; for this reason we’ll narrow the period search range for the sake of this example:

In [1]: from gatspy import datasets, periodic

In [2]: rrlyrae = datasets.fetch_rrlyrae()

In [3]: lcid = rrlyrae.ids[0]

In [4]: t, mag, dmag, filts = rrlyrae.get_lightcurve(lcid)

In [5]: mask = (filts == 'r')

In [6]: t_r, mag_r, dmag_r = t[mask], mag[mask], dmag[mask]

In [7]: model = periodic.SuperSmoother(fit_period=True)

In [8]: model.optimizer.period_range = (0.61, 0.62)

In [9]: model.fit(t_r, mag_r, dmag_r);

Now the best period is stored in a class attribute:

In [10]: model.best_period
Out[10]: 0.61432002634119753

Let’s take a look at the best-fit supersmoother model at this period:

(Source code, png, hires.png, pdf)

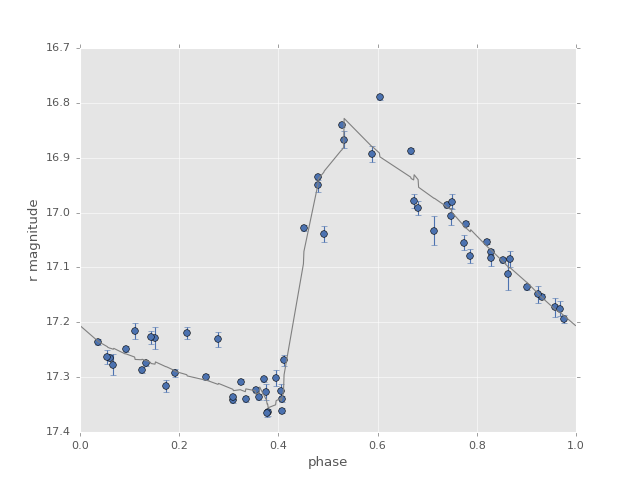
../_images/supersmoother-1.png

As you can see, the supersmoother method is very flexible and essentially creates a smooth nonparametric model at each frequency. We can construct the analog of the Lomb-Scargle periodogram using the supersmoother as well:

(Source code, png, hires.png, pdf)

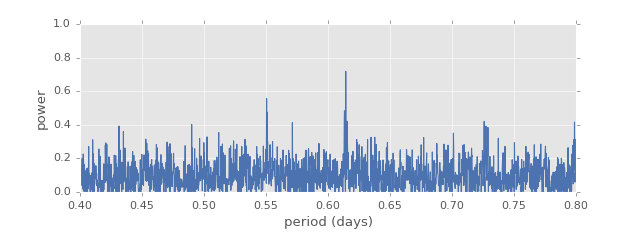
../_images/supersmoother-2.png

The supersmoother periodogram shows a clear spike at a period of around 0.62 days.

Multiband Supersmoother

The gatspy.periodic module also contains a multiband version of the supersmoother. Unlike the multiband lomb-scargle, there is no attempt here to make the smoothing on each band consistent: the multiband model consists of separate smooths on each band, with the weighted \chi^2 added to produce the final score. Here is an example of this periodogram computed on some test data:

(Source code, png, hires.png, pdf)

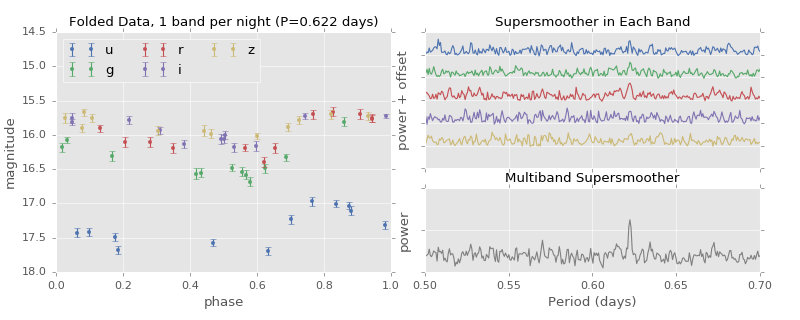
../_images/supersmoother-3.png

By combining the five models, we find a “periodogram” which isolates the unknown peak.