Decision Tree for RR Lyrae Classification¶
Figure 9.12
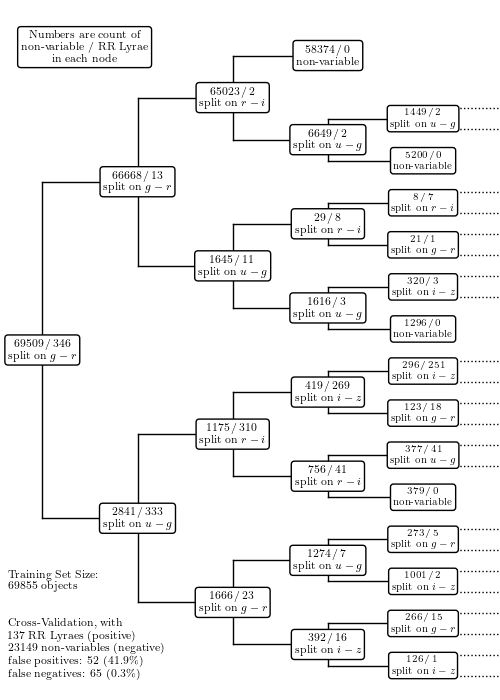
The decision tree for RR Lyrae classification. The numbers in each node are the statistics of the training sample of ~70,000 objects. The cross-validation statistics are shown in the bottom-left corner of the figure. See also figure 9.13.
----------------------------------------------------------------
partial training set: (69509 non-variable, 346 RR Lyrae)
positive = RR Lyrae, negative = non-variable
false positives: 52 (41.9%)
false negatives: 65 (0.3%)
----------------------------------------------------------------
full training set: (69509 non-variables, 346 RR Lyraes)
positive = RR Lyrae, negative = non-variables
false positives: 52 (41.9%)
false negatives: 65 (0.3%)
# Author: Jake VanderPlas
# License: BSD
# The figure produced by this code is published in the textbook
# "Statistics, Data Mining, and Machine Learning in Astronomy" (2013)
# For more information, see http://astroML.github.com
# To report a bug or issue, use the following forum:
# https://groups.google.com/forum/#!forum/astroml-general
from __future__ import print_function
import numpy as np
from matplotlib import pyplot as plt
from sklearn.tree import DecisionTreeClassifier
from astroML.datasets import fetch_rrlyrae_combined
from astroML.utils import split_samples
#----------------------------------------------------------------------
# This function adjusts matplotlib settings for a uniform feel in the textbook.
# Note that with usetex=True, fonts are rendered with LaTeX. This may
# result in an error if LaTeX is not installed on your system. In that case,
# you can set usetex to False.
if "setup_text_plots" not in globals():
from astroML.plotting import setup_text_plots
setup_text_plots(fontsize=8, usetex=True)
# % sign needs to be escaped if usetex is True
import matplotlib
if matplotlib.rcParams.get('text.usetex'):
pct = r'\%'
else:
pct = '%'
def get_x_position(level, n_levels, xmin=0.01, xmax=1):
dx = (xmax - xmin) / (n_levels - 1.)
return xmin + level * dx
def get_y_position(level, j, ymin=0, ymax=1):
n = 2 ** level
dy = (ymax - ymin) * 1. / n
return ymin + (j + 0.5) * dy
def draw_connections(x_positions, y_positions, children, i,
ax, linestyle='-k'):
for (c, y) in zip(children, y_positions):
if c == -1:
continue
ax.plot(x_positions[i - 1:i + 1], [y, y], linestyle, lw=1)
for j in range(0, 2 ** i, 2):
if children[j] == -1 or children[j + 1] == -1:
continue
ax.plot(2 * [x_positions[i - 1]], y_positions[j:j + 2],
linestyle, lw=1)
def visualize_tree(T, data, classes, labels=None, levels=5,
ymin=0, ymax=1, xmin=0, xmax=1, ax=None):
# to visualize the tree, we essentially need to re-build it: it doesn't
# store the list of points at each node.
if ax is None:
ax = plt.gca()
# get tree aspects
try:
# new versions of sklearn
T_children = T.tree_.children
except:
# old versions of sklearn
T_children = np.vstack([T.tree_.children_left,
T.tree_.children_right]).T
try:
# version < 0.14
T_nsamples = T.tree_.n_samples
except AttributeError:
# version 0.14+
T_nsamples = T.tree_.n_node_samples
T_feature = T.tree_.feature
T_threshold = T.tree_.threshold
x_positions = get_x_position(np.arange(levels + 1), levels)
node_list = np.array([0])
new_data_masks = [np.ones(data.shape[0], dtype=bool)]
for i in range(levels):
y_positions = get_y_position(i, np.arange(2 ** i))
mask = (node_list != -1)
# plot the positions of the nodes
ax.plot(x_positions[i] * np.ones(2 ** i)[mask],
y_positions[mask], 'ok')
data_masks = new_data_masks
new_data_masks = []
# list node info
for j in range(2 ** i):
if node_list[j] == -1:
new_data_masks += [None, None]
continue
ind = node_list[j]
# get masks of children
split_mask = (data[:, T_feature[ind]] < T_threshold[ind])
new_data_masks.append(np.logical_and(data_masks[j], split_mask))
new_data_masks.append(np.logical_and(data_masks[j], ~split_mask))
n_neg = np.sum(classes[data_masks[j]] == 0)
n_pos = np.sum(classes[data_masks[j]] == 1)
text = "$%i\,/\,%i$" % (n_neg, n_pos)
# assure that we're doing this correctly
assert (n_neg + n_pos == T_nsamples[ind])
# check if node is a leaf
if n_neg == 0:
text += "\n" + r"${\rm(RR\,Lyrae)}$"
elif n_pos == 0:
text += "\n" + r"${\rm non}$-${\rm variable}$"
else:
text += "\n" + r"${\rm split\ on}$ %s" % labels[T_feature[ind]]
if i < 4:
fontsize = 8
else:
fontsize = 7
ax.text(x_positions[i], y_positions[j], text,
ha='center', va='center',
fontsize=fontsize,
bbox=dict(boxstyle='round', ec='k', fc='w'))
# draw lines connecting nodes to parents
if i > 0:
draw_connections(x_positions, y_positions, node_list, i, ax, '-k')
# get next set of nodes
node_list = np.concatenate(list(T_children[node_list]))
# draw dotted line for last level
y_positions = get_y_position(levels, np.arange(2 ** levels))
draw_connections(x_positions, y_positions, node_list, levels, ax, ':k')
# set suitable axes limits
dx = 0.1 * (xmax - xmin)
dy = 0.02 * (xmax - xmin)
ax.set_xlim(xmin - dx, xmax + 2 * dx)
ax.set_ylim(ymin - dy, ymax + dy)
#----------------------------------------------------------------------
# get data and split into training & testing sets
X, y = fetch_rrlyrae_combined()
(X_train, X_test), (y_train, y_test) = split_samples(X, y, [0.75, 0.25],
random_state=0)
N_tot = len(y)
N_st = np.sum(y == 0)
N_rr = N_tot - N_st
N_train = len(y_train)
N_test = len(y_test)
N_plot = 5000 + N_rr
clf = DecisionTreeClassifier(random_state=0, criterion='entropy')
clf.fit(X_train, y_train)
y_out = clf.predict(X_test)
eq = (y_out == y_test)
#--------------------------------------------------
# compute statistics of cross-validation
tot_neg = np.sum(y_test == 0)
tot_pos = np.sum(y_test == 1)
fn = np.sum((y_test == 1) & (y_out == 0))
tn = np.sum((y_test == 0) & (y_out == 0))
fp = np.sum((y_test == 0) & (y_out == 1))
tp = np.sum((y_test == 1) & (y_out == 1))
print("----------------------------------------------------------------")
print("partial training set: (%i non-variable, %i RR Lyrae)"
% (np.sum(y_train == 0), np.sum(y_train == 1)))
print("positive = RR Lyrae, negative = non-variable")
print("false positives: %i (%.1f%%)" % (fp, fp * 100. / (fp + tp)))
print("false negatives: %i (%.1f%%)" % (fn, fn * 100. / (fn + tn)))
#------------------------------------------------------------
# Plot the results
fig = plt.figure(figsize=(5, 7), facecolor='w')
ax = fig.add_axes([0, 0, 1, 1], xticks=[], yticks=[], frameon=False)
visualize_tree(clf, X_train, y_train,
labels=(['$u-g$', '$g-r$', '$r-i$', '$i-z$']))
ax.text(0.12, 0.95, ("Numbers are count of\n"
"non-variable / RR Lyrae\n"
"in each node"),
ha='center', va='center',
bbox=dict(boxstyle='round', ec='k', fc='w'))
ax.text(-0.08, 0.14, ("Training Set Size:\n"
" %i objects" % len(y_train)),
ha='left', va='bottom')
ax.text(-0.08, 0.01, ("Cross-Validation, with\n"
" %i RR Lyraes (positive)\n"
" %i non-variables (negative)\n"
" false positives: %i (%.1f%s)\n"
" false negatives: %i (%.1f%s)"
% (tot_pos, tot_neg,
fp, fp * 100. / (tp + fp), pct,
fn, fn * 100. / (tn + fn), pct)),
ha='left', va='bottom')
#--------------------------------------------------
# compute statistics for a larger training set
clf = DecisionTreeClassifier(random_state=0, criterion='entropy')
clf.fit(X_train, y_train)
y_out = clf.predict(X_test)
tot_neg = np.sum(y_test == 0)
tot_pos = np.sum(y_test == 1)
fn = np.sum((y_test == 1) & (y_out == 0))
tn = np.sum((y_test == 0) & (y_out == 0))
fp = np.sum((y_test == 0) & (y_out == 1))
tp = np.sum((y_test == 1) & (y_out == 1))
print("----------------------------------------------------------------")
print("full training set: (%i non-variables, %i RR Lyraes)"
% (np.sum(y_train == 0), np.sum(y_train == 1)))
print("positive = RR Lyrae, negative = non-variables")
print("false positives: %i (%.1f%%)" % (fp, fp * 100. / (fp + tp)))
print("false negatives: %i (%.1f%%)" % (fn, fn * 100. / (fn + tn)))
plt.show()
