Cross Validation Examples: part 2

Figure 8.13

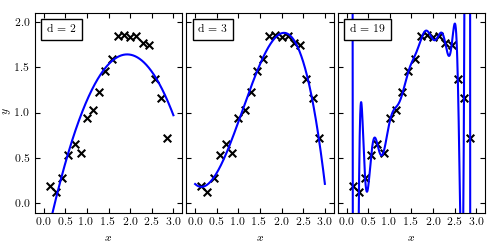
Three models of increasing complexity applied to our toy dataset (eq. 8.75). The d = 2 model, like the linear model in figure 8.12, suffers from high bias, and underfits the data. The d = 19 model suffers from high variance, and overfits the data. The d = 3 model is a good compromise between these extremes.

Code output:

Python source code:

# Author: Jake VanderPlas
# License: BSD
#   The figure produced by this code is published in the textbook
#   "Statistics, Data Mining, and Machine Learning in Astronomy" (2013)
#   For more information, see http://astroML.github.com
#   To report a bug or issue, use the following forum:
#    https://groups.google.com/forum/#!forum/astroml-general
import numpy as np
from matplotlib import pyplot as plt
from matplotlib import ticker
from matplotlib.patches import FancyArrow

#----------------------------------------------------------------------
# This function adjusts matplotlib settings for a uniform feel in the textbook.
# Note that with usetex=True, fonts are rendered with LaTeX.  This may
# result in an error if LaTeX is not installed on your system.  In that case,
# you can set usetex to False.
if "setup_text_plots" not in globals():
    from astroML.plotting import setup_text_plots
setup_text_plots(fontsize=8, usetex=True)


#------------------------------------------------------------
# Define our functional form
def func(x, dy=0.1):
    return np.random.normal(np.sin(x) * x, dy)

#------------------------------------------------------------
# select the (noisy) data
np.random.seed(0)
x = np.linspace(0, 3, 22)[1:-1]
dy = 0.1
y = func(x, dy)

#------------------------------------------------------------
# Select the cross-validation points
np.random.seed(1)
x_cv = 3 * np.random.random(20)
y_cv = func(x_cv)

x_fit = np.linspace(0, 3, 1000)

#------------------------------------------------------------
# Second figure: plot fit for several orders of polynomial
fig = plt.figure(figsize=(5, 2.5))
fig.subplots_adjust(wspace=0.03, bottom=0.15,
                    top=0.95, left=0.07, right=0.97)

for i, d in enumerate([2, 3, 19]):
    ax = fig.add_subplot(131 + i)
    ax.scatter(x, y, marker='x', c='k', s=30)

    p = np.polyfit(x, y, d)
    y_fit = np.polyval(p, x_fit)

    ax.plot(x_fit, y_fit, '-b')
    ax.set_ylim(-0.1, 2.1)
    ax.set_xlim(-0.2, 3.2)
    if i in (1, 2):
        ax.yaxis.set_major_formatter(plt.NullFormatter())
    else:
        ax.set_ylabel('$y$')
    ax.set_xlabel('$x$')
    ax.text(0.08, 0.94, "d = %i" % d, transform=ax.transAxes,
            ha='left', va='top',
            bbox=dict(ec='k', fc='w'))

plt.show()

[download source: fig_cross_val_B.py]