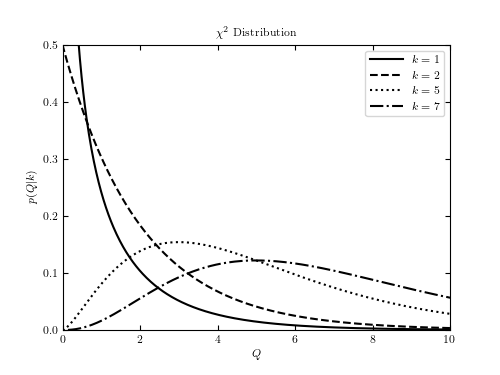
Example of a chi-squared distribution

Figure 3.14.

This shows an example of a 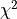distribution with various parameters. We’ll generate the distribution using:

dist = scipy.stats.chi2(...)

Where … should be filled in with the desired distribution parameters Once we have defined the distribution parameters in this way, these distribution objects have many useful methods; for example:

• dist.pmf(x) computes the Probability Mass Function at values x in the case of discrete distributions

• dist.pdf(x) computes the Probability Density Function at values x in the case of continuous distributions

• dist.rvs(N) computes N random variables distributed according to the given distribution

Many further options exist; refer to the documentation of scipy.stats for more details.

Code output:

Python source code:

# Author: Jake VanderPlas
# License: BSD
#   The figure produced by this code is published in the textbook
#   "Statistics, Data Mining, and Machine Learning in Astronomy" (2013)
#   For more information, see http://astroML.github.com
#   To report a bug or issue, use the following forum:
#    https://groups.google.com/forum/#!forum/astroml-general
import numpy as np
from scipy.stats import chi2
from matplotlib import pyplot as plt

#----------------------------------------------------------------------
# This function adjusts matplotlib settings for a uniform feel in the textbook.
# Note that with usetex=True, fonts are rendered with LaTeX.  This may
# result in an error if LaTeX is not installed on your system.  In that case,
# you can set usetex to False.
if "setup_text_plots" not in globals():
    from astroML.plotting import setup_text_plots
setup_text_plots(fontsize=8, usetex=True)

#------------------------------------------------------------
# Define the distribution parameters to be plotted
k_values = [1, 2, 5, 7]
linestyles = ['-', '--', ':', '-.']
mu = 0
x = np.linspace(-1, 20, 1000)

#------------------------------------------------------------
# plot the distributions
fig, ax = plt.subplots(figsize=(5, 3.75))
fig.subplots_adjust(bottom=0.12)

for k, ls in zip(k_values, linestyles):
    dist = chi2(k, mu)

    plt.plot(x, dist.pdf(x), ls=ls, c='black',
             label=r'$k=%i$' % k)

plt.xlim(0, 10)
plt.ylim(0, 0.5)

plt.xlabel('$Q$')
plt.ylabel(r'$p(Q|k)$')
plt.title(r'$\chi^2\ \mathrm{Distribution}$')

plt.legend()
plt.show()

[download source: fig_chi2_distribution.py]