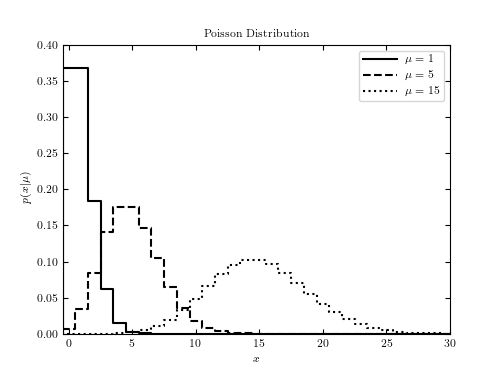
Example of a Poisson distribution

Figure 3.10.

This shows an example of a Poisson distribution with various parameters. We’ll generate the distribution using:

dist = scipy.stats.poisson(...)

Where … should be filled in with the desired distribution parameters Once we have defined the distribution parameters in this way, these distribution objects have many useful methods; for example:

• dist.pmf(x) computes the Probability Mass Function at values x in the case of discrete distributions

• dist.pdf(x) computes the Probability Density Function at values x in the case of continuous distributions

• dist.rvs(N) computes N random variables distributed according to the given distribution

Many further options exist; refer to the documentation of scipy.stats for more details.

Code output:

Python source code:

# Author: Jake VanderPlas
# License: BSD
#   The figure produced by this code is published in the textbook
#   "Statistics, Data Mining, and Machine Learning in Astronomy" (2013)
#   For more information, see http://astroML.github.com
#   To report a bug or issue, use the following forum:
#    https://groups.google.com/forum/#!forum/astroml-general
import numpy as np
from scipy.stats import poisson
from matplotlib import pyplot as plt

#----------------------------------------------------------------------
# This function adjusts matplotlib settings for a uniform feel in the textbook.
# Note that with usetex=True, fonts are rendered with LaTeX.  This may
# result in an error if LaTeX is not installed on your system.  In that case,
# you can set usetex to False.
if "setup_text_plots" not in globals():
    from astroML.plotting import setup_text_plots
setup_text_plots(fontsize=8, usetex=True)

#------------------------------------------------------------
# Define the distribution parameters to be plotted
mu_values = [1, 5, 15]
linestyles = ['-', '--', ':']

#------------------------------------------------------------
# plot the distributions
#   we generate it using scipy.stats.poisson().  Once the distribution
#   object is created, we have many options: for example
#   - dist.pmf(x) evaluates the probability mass function in the case of
#     discrete distributions.
#   - dist.pdf(x) evaluates the probability density function for
#   evaluates
fig, ax = plt.subplots(figsize=(5, 3.75))

for mu, ls in zip(mu_values, linestyles):
    # create a poisson distribution
    # we could generate a random sample from this distribution using, e.g.
    #   rand = dist.rvs(1000)
    dist = poisson(mu)
    x = np.arange(-1, 200)

    plt.plot(x, dist.pmf(x), color='black',
             linestyle='steps-mid' + ls,
             label=r'$\mu=%i$' % mu)

plt.xlim(-0.5, 30)
plt.ylim(0, 0.4)

plt.xlabel('$x$')
plt.ylabel(r'$p(x|\mu)$')
plt.title('Poisson Distribution')

plt.legend()
plt.show()

[download source: fig_poisson_distribution.py]